Taking use of stack: the longest valid parentheses sequence problem

I practice on Acwing and a problem stucked me. In fact, the problem is not so difficult as I imagined. Instead, it is an application of stack.

The Logest Valid Parentheses Problem

A valid parentheses sequence satisfies the following conditions.

• The string "()" is considered legal.
• If the strings "X" and "Y" are legal, then "XY" is also considered legal.
• If the string "X" is legal, then "(X)" is also legal.

For example, (), ()(), (()) These are all legal.

Now, given a string S consisting of "(" and ")".

You are asked to find the length of the longest valid parentheses sequence in it and the count of them.

Input format

A string consisting of ( and ) in one line.

Output format

A line of two integers indicating the length and number of the longest valid parentheses sequence.

If no valid parentheses sequence exists, 0 1 should be outputed.

Data range

The first six test points satisfy: 1 ≤ |S| ≤ 100. All test points satisfy: 1≤|S|≤106.

Ideas

When it comes to judging if a parentheses sequence is valid, we always think of using stack. However, in this problem, we are supoosed not only to judge it but also output the length and count of the longest valid parentheses sequence. Since the data is big ($10^{6}$), it would exceed the time limit.

We could draw a picture to help us to think about this problem.

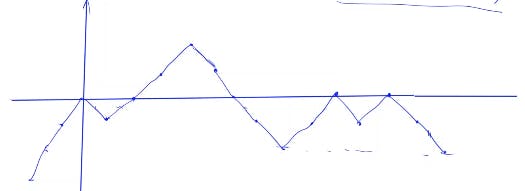
In this picture, we could regard each parentheses as a point of the line, which has its own valud value 1 of "(" and value -1 of ")". If there are two parentheses A and B that construct makes the sequence between them valid, the vertical indices of them should be the same. Futhermore, each point between them should have its vertical index no less than A and B.

Therefore, we could regard the matching process as eliminating parentheses. If we find a point B that has the same vertical index as A and the next point of B has lower vertical index than A, then we can say we find a locally longgest valid parentheses squence. After that, we set the next point of B as A and search for next match.

code

#include <iostream>
#include <algorithm>
#include <stack>

using namespace std;

stack<int> st;

string s;

int main(){
    cin >> s;

    int rl = 0, rc = 1;
    for(int i = 0; i < s.size(); i++){
        if(!st.empty() && s[st.top()] == '(' && s[i] == ')'){
            st.pop();
        }
        else{
            st.push(i); // here we use index to record whether the parentheses is '(' or ')'
        }

        int r;
        if(!st.empty()){
            r = i - st.top();
        }
        else{
            r = i + 1;
        }

        if(r > rl){
            rl = r;
            rc = 1;
        }
        else if(r == rl){
            rc++;
        }
    }
    if(rl == 0){
        cout << "0 1";
    }
    else{
        cout << rl << " " << rc;
    }
}